Base pump, WV, μmol/J, phosphor CE, LED effeciency

Just a quick little post on LED effeciency.

Phosphor conversion effeciencies (CE) are never over 1. They approach 1, but never exceed 1 (about 99.9%). This essentially means that photons emitted are maintained, ie the phosphor film doesn't diminish the initial photon quantity, all photons are conserved.

A white LED uses a blue pump, or a blue "base" diode to create the initial quantity of photons, and then the phosphor film layer converts all the blue photons created by the base pump to all sorts of different color photons.

Every photons' WV has a unique energy associated with it. This energy can be expressed in terms of μmol/J, or the amount of energy (J) per photon qty (μmol). A 450nm photon will have a higher and different distinct energy than a 451nm. A 646nm has its distinct energy, a 757nm photon has its distinct energy, ect ect. If the WV changes so does the energy. This energy can be easily calculated with the 119.3 conversion factor.

119.3 ÷ WV = J/μmol
WV ÷ 119.3 = μmol/J

Example:
455nm ÷ 119.3 = 3.81μmol/J
119.3 ÷ 455nm = 0.262J/μmol

445nm ÷ 119.3 = 3.73μmol/J
119.3 ÷ 445nm = 0.268μmol/J

With just a 10nm difference in base pump one can see a diminished photon effeciency of one over the other. Which would you rather have, 3.81 or 3.73?

To determine % effeciency of an LED given in μmol/J, you'd want to find the peak WV of the base pump by looking at the SPD on the datasheet. Then you'd divide the peak base pump WV by 119.3 to achieve the max possible μmol/J, and then you'd look at the data sheet for what it says it's μmol/J effeciency is.

Example:
80CRI 3500k LM301h rated @ 2.67 μmol/J


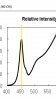
Looks like peak base pump WV is around 455nm.

455 ÷ 119.3 = 3.81μmol/J

(2.67 μmol/J) ÷ (3.18μmol/J)
=
0.70 or 70% effecient

At 70% effeciency, ~30% of consumed power would need to be calculated for heatsink needs. There will be some additional heat losses on the phosphor film due to conversion though and I'm not exactly sure what percentage of the remaining 70% will be converted to heat (maybe 5%, maybe 10%, it'll be dependepent on SPD). The farther the conversion, ie the farther away from the base pump WV, the higher the heat loss on the phosphor film.

Because the conversion factor (119.3) never changes you can easily compare WV photon effeciencies by simply comparing their WVs.
650nm ÷ 450nm = 1.44, this means that if 2 chips were present, both having equal effeciencies and power consumption rates but different WVs, ie 1 is a 450nm chip and 1 is a 650nm chip, the 650nm chip will produce 1.44x more photons than the 450nm chip (144%).

Good stuff Chief, always nice to see you around.

What is WV?

Where did you get the 119.3 conversion factor?
I would think the conversion factor would be dependent on the ratio of green and red phosphors and the efficiency and bandwidth of each phosphor used.

I'm not sure what your point is to the 10 nm change in base wavelength.
Manufacturers put a lot of effort into making the most efficient deep blue LED.
The most efficient wavelength is determined by the materials.
It's not like you can pick and choose the desired base wavelength.

With regards to the 70% efficiency and 30% heat is correct if the efficiency is total external quantum efficiency.
You measure the the number of election entering and number of photons exiting the LED.
There is much more to the internal efficiencies than just phosphor conversion.
There is the efficiency of converting elections to photons.
There is quantum well efficiency for the number of photons that do not exit the well never reaching the phosphor.
Bottom line a photon either exits the LED or is converted to heat.

ChiefRunningPhist said:

Phosphor conversion efficiencies (CE) are never over 1

Click to expand...

Theoretically phosphor wavelength down conversion efficiency could, and may someday, exceed 1.
You are converting a deep blue photon to a lower energy photon.

eatled said:

What is WV?

Where did you get the 119.3 conversion factor?
I would think the conversion factor would be dependent on the ratio of green and red phosphors and the efficiency and bandwidth of each phosphor used.

I'm not sure what your point is to the 10 nm change in base wavelength.
Manufacturers put a lot of effort into making the most efficient deep blue LED.
The most efficient wavelength is determined by the materials.
It's not like you can pick and choose the desired base wavelength.

With regards to the 70% efficiency and 30% heat is correct if the efficiency is total external quantum efficiency.
You measure the the number of election entering and number of photons exiting the LED.
There is much more to the internal efficiencies than just phosphor conversion.
There is the efficiency of converting elections to photons.
There is quantum well efficiency for the number of photons that do not exit the well never reaching the phosphor.
Bottom line a photon either exits the LED or is converted to heat.


Theoretically phosphor wavelength down conversion efficiency could, and may someday, exceed 1.
You are converting a deep blue photon to a lower energy photon.

Click to expand...

119.6 ... Oops!

WV = wavelength

It could but its not even 1 yet. I deal with current technology so I'm not going to estimate something that doesn't exist.

You're confusing the different effeciency metrics. The 119.6 conversion factor isn't determined by the phosphor, it's determined by the physics of light. The electrical effeciency of the light then cuts into this figure.

A CE is determined by the phosphor and the body of the LED, I'm giving the benefit of the doubt when I say CE is 1. Most LED CE will be close to 1, but never over. A CE if less than 1, would further cut into the (WV/119.6) figure aditional to electrical effeciency losses.

As far as the 10nm base pump it does make a difference. They bin the base pumps by nm of emmision. Samsung doesn't use lower nm base pumps than what they do because their total μmol would be less. When the market is as close as it is, a few nm difference in base pump can be the differnce in being #1 or #2 most effecient. If both LED bodies or wells are the same effeciency and both have the same phosphor and phosphor thickness then a lower nm base pump LED will have less μmol/s output than a higher base pump LED. The base chips are the same, they are all InGaN, so a bit of a different epitaxial growth structure creates a bit of variability but they are the same material.

BTW its a good thing you asked about the conversion factor, looks like I was off by 0.3! Check my math..

Try it out if you don't think it's correct, then google your result. I went to school for engineering but sometimes I make mistakes.. 0.3! Eek!

diggs99 said:

Good stuff Chief, always nice to see you around.

Click to expand...

Thanks man! Hope all is well! Just been trying to get this light built..

I am impressed with your work. Not many understand this stuff, especially on this site.

My conversion factor from watts to µmol/s is 3.8 and .26 µmol to watts/s.
The way I do it is to calculate 1 radiant watt, 1 µmol, and 1 lux.
In this table I convert from Lux, watts, and µmol. The right most columns are calculated values compared to measured values using a spectrometer (NIST traceable), as my verification.

My PHP formulas for the watt to µmol and lux calculations where $cie[] is the CIE Photopic Luminous Efficacy for each wavelength.

$watts = 1;
$ppf = $watts * 0.00836 * $wavelength;
$lux = $ppf * $cie[$wavelength] / ($wavelength * 0.00836) * 683;

________________________________________________________________

0.00836 was derived by simplifying h•(c/λ)

The energy of a mole of photons of a given wavelength is Ep•NA (NA=6,022•10^23 mol-1).

The number of photons Np per second and surface unit can be calculated from the irradiance (I) by (note: the nm value for λ is used):
Np= I/Ep= I•((λ•10-9)/h•c) = I [W/m2]•λ•10^-9[m]•/ (1.988•10^-25) [J•m]
= I•λ•5.03•10^15 [1/(m²•s)]

The photon flux can be determined by converting the number of photons to µmoles of photons:
EQF = Np/(NA•10^6) (with Avogadro number NA=6,022•10^23 mol-1) / m•s

Taken together this leads to the following equation for converting irradiance [W/m²] into quantum flux [µE]:
EQF = (I•λ•5.03•10^15[1/(m²•s)])/(6.02•10^17[1/µmol])
= I•λ•0.836•10-2 [µmol/(m²•s) = µE]

Well don't know much about PHP :/ but ya I was trying to find the equation of the Luminosity curve so I could find the exact lm/nm multiplier, but never found it. I tried to model the Luminosity curve after a normal distribution curve, but found a tool that seemed to do what I wanted so I just left it be.

Curious though, how did you find the CIE for each nm? And 683 must be the maximum lm multiplier?

Also how are you arriving at 0.00836, and where does 5.03 come from?
Does...

eatled said:

5.03•1015

Click to expand...

... mean 5.03e15 ?

If not where does (1015) come from?

I need to get into programming with something like PHP, very cool that you're able to make a program like that! I checked 1 data point for things I know to be certain (μmol/J/nm, mW/μmol/nm) and it matches exactly with what I calculate, so I'm more inclined to trust the lumen conversions, but like to know the nitty gritty behind it.

Never had the pleasure I don't believe, nice to to see some physics minds around

Your going to have to make me change my cheat sheet lol, I must have been using a rounded figure.. 119.3 smh..

Just some more cheating lol..

This is the last of the cheat sheets..

Some CV driver data sheets...

Some CC driver effeciencies...

Some CV driver effeciencies...

There is no formula. It's just a table.
Import the attached TXT file as a CSV.

ChiefRunningPhist said:

If not where does (1015) come from?

Click to expand...

ten to the fifteenth


Did a copy and paste which lost the super script. Added ^ where needed.

Better yet here is the page I learned it from years ago. The company had a different name then.

I made a spreadsheet with their formulas and tweaked it until my results matched their examples.

LINK: https://www.berthold-bio.com/service-support/support-portal/knowledge-base/how-do-i-convert-irradiance-into-photon-flux.html

ChiefRunningPhist said:

don't know much about PHP

Click to expand...

Conversion:

µmol = watts × 0.00836 × wavelength in nm;

ChiefRunningPhist said:

Your going to have to make me change my cheat sheet

Click to expand...

Not too much. The reciprocal of 0.00836 = 0.001196

You could just change × to ÷ and move the decimal point

ChiefRunningPhist said:

I was trying to find the equation of the Luminosity curve

Click to expand...

There is no formula. It's a table.

Import the attached TXT as a CSV

ChiefRunningPhist said:

And 683 must be the maximum lm multiplier?

Click to expand...

The human eye is most sensitive to 555 nm green.

The standard luminosity function is normalized to a peak value of unity at 555 nm (see luminous coefficient). The value of the constant in front of the integral is usually rounded off to 683 lm/W. The small excess fractional value comes from the slight mismatch between the definition of the lumen and the peak of the luminosity function. The lumen is defined to be unity for a radiant energy of 1/683 W at a frequency of 540 THz, which corresponds to a standard air wavelength of 555.016 nm rather than 555 nm, which is the peak of the luminosity curve.

Source: Wikipedia

Photopic Luminous Efficacy comes from the Relative Sensitivity Curve for the C.I.E. Standard Observer
555 nm green was compared with other colors and observed by a bunch of people (aka standard observer). The brightness of the 555 nm source was reduced until the observer felt that the two sources were equal in brightness. The fraction by which the 555 nm source was reduced, became the luminous sensitivity with respect to the second observed wavelength.

Have you seen this thread by @alesh https://www.rollitup.org/t/math-behind.868988/

eatled said:

Have you seen this thread by @alesh https://www.rollitup.org/t/math-behind.868988/

Click to expand...

I hadn't seen that particular thread but have tried to reach out to @alesh and the supra guy. It seems they just do the labor of finding every lm output per nm for a specific SPD and then use excel to multiply by the CIE factor.

I was trying to use the actual equations of the curves, the Luminosity curve, and the SPD curve, multiply them and integrate from bottom WV emission to top WV emission. I was using techniques I learned in school to approximate curve equations from a visual representation, (asymptotes, parabolas, normal curves, ect), but these proved harder to approximate than anticipated (or remember how lol) and I found a tool that seemed to do what I needed to find the conversion without the calculus, or me personally digitizing (someone probably already had done it).

I've been wanting to bounce shit off of them for awhile but they don't seem to be around anymore. This technique was one of those ideas.

The attached PDF has a lot of information regarding phosphor wavelength converters.